几何着色器

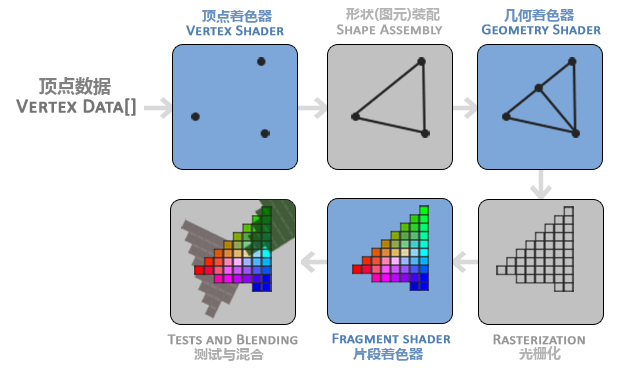
从openGL的渲染管线图中可以看出，其实在顶点着色器和片段着色器之间还隐藏着一个着色器——几何着色器。这个着色器并不是必须的，如果不主动提供给openGL，它便会自己生成一个最基本几何着色器，即对顶点不做任何变换。

从它的名字也可以很容易看出，几何着色器主要是针对物体进行变换的。与顶点着色器中的模型矩阵不同的是，模型矩阵是针对所有顶点进行变换，而几何着色器甚至可以精确到每一个顶点。

几何着色器处理的对象是图元，也即是构成模型最基本的图形，这里可以是三角形，点或者是线段。通过对图元的操作，几何着色器可以将图元形状改变，抑或是增加图元的顶点或移动图元。几何着色器这种更改图元的方式相比直接修改原模型顶点要高效很多，因为这是GPU在处理。下面通过两个具体的例子来说明几何着色器的作用。

物体爆破特效

物体爆破特效在游戏中经常被用到，例如对墙体的爆破等等。这些特效大多都是用几何着色器来实现，虽然无法复刻像游戏那样的爆破效果，但是我们还是可以尝试写一个简单的爆破特效。思路是：将mesh里面的每个图元都沿法线方向位移，这样便可以呈现出物体沿法线膨胀开裂的效果。

#version 330 core
layout(triangles) in;
layout(triangle_strip,max_vertices=3) out;

in VS_OUT{
    vec2 Texcoord;
    vec3 Normal;
    vec3 Pos;
}gs_in[];

out GS_OUT{

    vec2 Texcoord;
    vec3 Normal;
    vec3 Pos;

}gs_out;

uniform float time;
uniform mat4 Model;
uniform mat4 View;
uniform mat4 Projection;
vec3 getExplodeVec(vec3 normal,vec3 positon){
    vec3 result;
    float magnitude=2.f;
    result=positon+((sin(time)+1.f)/2.f)*magnitude*normal;
    return result;
}

vec3 getNormal(){
    vec3 a=gs_in[0].Pos-gs_in[1].Pos;
    vec3 b=gs_in[1].Pos-gs_in[2].Pos;
    vec3 result=normalize(cross(a,b));
    
    return result;
}

void main(){

    vec3 tmppos;
    vec3 normal=getNormal();
    tmppos=getExplodeVec(gs_in[0].Normal,gs_in[0].Pos);
    gl_Position=Projection*View*vec4(tmppos,1.f);
    gs_out.Texcoord=gs_in[0].Texcoord;
    gs_out.Normal=gs_in[0].Normal;
    gs_out.Pos=gs_in[0].Pos;
    EmitVertex();

    tmppos=getExplodeVec(gs_in[0].Normal,gs_in[1].Pos);
    gl_Position=Projection*View*vec4(tmppos,1.f);
    gs_out.Texcoord=gs_in[1].Texcoord;
    gs_out.Normal=gs_in[1].Normal;
    gs_out.Pos=gs_in[1].Pos;
    EmitVertex();

    tmppos=getExplodeVec(gs_in[0].Normal,gs_in[2].Pos);
    gl_Position=Projection*View*vec4(tmppos,1.f);
    gs_out.Texcoord=gs_in[2].Texcoord;
    gs_out.Normal=gs_in[2].Normal;
    gs_out.Pos=gs_in[2].Pos;
    EmitVertex();

    EndPrimitive();

}

首先看前两行，这里的layout是指定输入和输出图元的类型，triangles表明输入的图元是三角形，而triangle_strip表明输出的图元也是三角形，而且是三角形带。这里补充一下对三角形带的说明，三角形顾名思义就是三角形组成的带状，其绘制方式可以这样理解，首先先绘制出一个三角形，然后再三角形外部再绘制一个顶点，然后以已经存在的三角形的一条边，再绘制出一个新的三角形，然后循环这个过程，最后便可以得到一个三角形带。最后max_vertices则表示最多绘制的顶点数目，超过这个数目后openGL将不再进行绘制。
然后再看第一个输入块

in VS_OUT{
    vec2 Texcoord;
    vec3 Normal;
    vec3 Pos;
}gs_in[];

这是从顶点着色器输入的数据块，这里要注意的是几何着色器的输入都是数组，因为图元大多数都是一个以上的点组成的，并且即是图元就是点类型，还是需要以数组输入，只不过数组里面只有一个元素。

主函数里面一共出现了三次EmitVertex()函数，这是将顶点数据继续发送给下一个着色器，不过我猜测这里的发送并不是直接就将这个顶点发送出去，而是先放在一个类似缓冲区的地方，然后等到调用EndPrimitive()才真正将顶点数据发送出去。最后将三角形的三个顶点都沿着其法线位移之后，几何着色器的任务也便完成了。
这就是最后渲染出来的效果

可以看到这种效果其实并不太像爆炸，或者说被炸成渣了，类似湮灭的效果。

向量可视化

向量可视化是几何着色器的另外一个应用，顾名思义，向量可视化就是让法向量可视，即染上一种颜色，效果就好像物体上长满了沿着法向量的毛一样。向量可视化的思路是这样的：首先先正常渲染出原物体，然后将glDrawArrays()的渲染图元改成GL_POINTS即点，然后利用几何着色器将每个点沿着法向量移动一小段距离，然后输出成一条线段，这样最后就可以呈现出可视化法向量的效果。

#version 330 core

layout(points) in;
layout(line_strip,max_vertices=2) out;

in VS_OUT{

    vec2 Texcoord;
    vec3 Normal;
    vec3 Pos;

}gs_in[];


uniform mat4 View;
uniform mat4 Model;
uniform mat4 Projection;

vec3 getOffsetVec(vec3 position,vec3 normal){
    vec3 result;
    float magnitude=0.3f;
    normal=normalize(normal);
    result=position+normal*magnitude;
    return result;
}

void main(){

    gl_Position=Projection*View*vec4(gs_in[0].Pos,1.f);
    EmitVertex();

    vec3 offsetVec=getOffsetVec(gs_in[0].Pos,gs_in[0].Normal);
    gl_Position=Projection*View*vec4(offsetVec,1.f);
    EmitVertex();

    EndPrimitive();
}

最后渲染出来的效果就是这样的